Modeling Heat Flow - Part 2

Background

Previously, I modeled a “hot box”, but ignored the effects of the sun. As anyone who has had to get into a car that has sat outside for a while on a hot summer day, the inside of the car is warmer than the outside air temperature, and my previous model didn’t allow that. So the sun is important. Consider the following information from The Humane Society.

It doesn’t have to be that warm outside for a car to become dangerously hot inside.

• When it’s 72 degrees Fahrenheit outside, the temperature inside your car can heat up to 116 degrees Fahrenheit within an hour.
• When it’s 80 degrees Fahrenheit outside, the temperature inside your car can heat up to 99 degrees Fahrenheit within 10 minutes.
• Rolling down the windows has been shown to have little effect on the temperature inside a car.

Let’s translate these temperatures to Celsius and Kelvin

• When it’s 22 degrees Celsius outside, the temperature inside your car can heat up to 47 degrees Celsius within an hour.
• When it’s 27 degrees Celsius outside, the temperature inside your car can heat up to 37 degrees Celsius within 10 minutes.

My plan for this post is to assume that my heat box will heat up similarly to the above generic car, and see what sort of parameters I need to make that work.

Previous work

As before, I’ll model the system as a simple box, however, this time it will be car-sized, and I’ll use thermal properties that are common for metals like aluminum, rather than parameters used for building materials.

import numpy as np

# Heat parameters
thermalDiffusivity = 22.39e-6 # meters^2/s for air
heatTransferCoef = 1 # For a typical metal to air W/m^2K
thermalConductivity = 50 # For a typical metal W/mK
specificHeat = 1000 # for aluminum J/kg K
wallDensity = 3000 # kg/m^3 for aluminum
solarIntensity = 1000 # W/m^2

# Length parameters (meters)
L = 3
W = 2
H = 1.5

Deltax = 0.05
xmax = int(L/Deltax)
ymax = int(W/Deltax)
zmax = int(H/Deltax)

xmid = xmax // 2
ymid = ymax // 2
zmid = zmax // 2

xgrid = np.linspace(0,L,xmax+1)
ygrid = np.linspace(0,W,ymax+1)
zgrid = np.linspace(0,H,zmax+1)

u0 = np.empty((xmax,ymax,zmax))

Heat Equation

The heat equation is:

\[ \frac{\partial u}{\partial t} = \alpha \nabla^2u + \text{Internal Power Generation Term} + \text{Convection on the boundary} \]

Where \(\alpha=\frac{k}{c\rho}\) is the thermal diffusivity of the material, and \(k\) is the thermal conductivity, \(c\) is the specific heat, and \(\rho\) is the density. The internal power generation term is going to be related to heat generation due to the absorption of sunlight, and will only be important on surfaces exposed to sunlight. The Boundary convection term will be, again only important on the exterior of the object being modeled. I’ll describe these terms in more detail later in this post.

When working numerically, it is common to employ a finite mesh of points and determine the system temperature at each of these points in space as follows: \[ u(x,y,z,t) \rightarrow u(x_i,y_j,z_k,t) = u_{i,j,k}(t) \]

I will create this 3D array of functions in time, rather than a 4D array, with one of the dimensions being the evolution in time because when solving differential equations, it is often important to adjust the time step to suit the numerical needs of the system. This way, I will be able to use numerical differential equation solvers as I tackle this problem.

Internal Power Generation

This should be proportional to the solar intensity. At the surface of the earth, the intensity of sunlight on a clear day is about 1000 \(\text{W}/\text{m}^2\). For now, I will model it as:

\[ A I_{\text{sun}} f(x,y,z) \]

where \(A\) is a constant that I will determine empirically. For this model, I will assume:

\[ f(x,y,z) = \begin{cases} 1 &z=H \\ 0 &\text{else} \end{cases} \]

This has the meaning that for this model, the sun is directly overhead, and sunlight is only incident on the top of the box. The constant \(A\) should depend on material properties like specific heat and density as follows:

\[ A = \frac{1}{c\rho\delta_{\text{eff}}} \]

where \(\delta_{\text{eff}}\) is an effective depth that the sunlight penetrates.

def powerGen(umat, t, intensity, A):
    powerGen = np.zeros_like(umat)

    powerDensity = A*intensity
    powerGen[:,:,-1].fill(powerDensity)

    return powerGen

Boundary convection

The power exchange per unit volume due to convection is proportional to the difference in temperature of air and the temperature at the boundary:

\[ B \left(T_{\text{air}}-u(x_S,y_S,z_S,t)\right) \]

for points \((x_S,y_S,z_S)\) on the boundary of the object (assuming a uniform air temperature). Again, \(B\) is a constant that I will determine empirically. However, the constant \(B\) should depend on material properties like specific heat, density, and the heat transfer coefficient as follows:

\[ B = \frac{h}{c\rho\Delta_{\text{eff}}} \]

where \(\Delta_{\text{eff}}\) is an effective thickness of the convection surface.

def bdryConv(umat, t, Tair, B):

    bdryTemp = np.zeros_like(umat)
    uSurf = np.zeros_like(umat)

    bdryTemp[0,:,:].fill(Tair)
    bdryTemp[:,0,:].fill(Tair)
    bdryTemp[:,:,0].fill(Tair)
    bdryTemp[-1,:,:].fill(Tair)
    bdryTemp[:,-1,:].fill(Tair)
    bdryTemp[:,:,-1].fill(Tair)

    uSurf[0,:,:] = umat[0,:,:]
    uSurf[:,0,:] = umat[:,0,:]
    uSurf[:,:,0] = umat[:,:,0]
    uSurf[-1,:,:] = umat[-1,:,:]
    uSurf[:,-1,:] = umat[:,-1,:]
    uSurf[:,:,-1] = umat[:,:,-1]

    duConvdt = B*(bdryTemp - uSurf)
    return duConvdt  

Laplacian

Lastly I have to deal with the Laplacian in the following cases:

1. Interior points
2. Boundary surfaces
3. Boundary edges
4. Boundary corners

In the finite difference method, the Laplacian is proportional to the average deviation of the current point from the nearest neighbors. I’ll show how this is calculated in later sections for surfaces, edges and corners. All in all this is quite tedious, and if you want to skip the math, navigate to the Analysis Plan section through the menu at the right.

Heat Equation on the interior of the box

The heat equation on the interior of the box has none of the contributions from the boundary terms: \[ \frac{\partial u(x,y,z,t)}{\partial t} = \alpha\nabla^2 u(x,y,z,t) \]

When we apply the finite element approximation, we get the following:

\[\begin{align*} \nabla^2 u(x,y,z,t) \rightarrow \frac{1}{\Delta x\Delta y\Delta z} &\left(\Delta y \Delta z \frac{u_{i-1,j,k}(t) + u_{i+1,j,k}(t) - 2 u_{i,j,k}(t)}{\Delta x} \right.\\ &\quad + \Delta x \Delta z \frac{u_{i,j-1,k}(t) + u_{i,j+1,k}(t) - 2 u_{i,j,k}(t)}{\Delta y} \\ &\qquad \left. + \Delta x \Delta y \frac{u_{i,j,k-1}(t) + u_{i,j,k+1}(t) - 2 u_{i,j,k}(t)}{\Delta z}\right) \\ \end{align*}\]

This simplifies to: \[\begin{align*} \nabla^2 u(x,y,z,t) &\rightarrow \frac{u_{i-1,j,k}(t) + u_{i+1,j,k}(t) - 2 u_{i,j,k}(t)}{\Delta x^2} \\ &\quad +\frac{u_{i,j-1,k}(t) + u_{i,j+1,k}(t) - 2 u_{i,j,k}(t)}{\Delta y^2} \\ & \qquad + \frac{u_{i,j,k-1}(t) + u_{i,j,k+1}(t) - 2 u_{i,j,k}(t)}{\Delta z^2} \end{align*}\]

If we generate our grid with \(\Delta x = \Delta y = \Delta z\), we obtain:

\[ \nabla^2 u_{i,j,k} = \frac{u_{i-1,j,k} + u_{i+1,j,k} + u_{i,j-1,k} + u_{i,j+1,k} + u_{i,j,k-1} + u_{i,j,k+1} - 6 u_{i,j,k}}{\Delta x^2} \\ \]

Heat Equation on a boundary surface

So if we are considering the \(x=0, i=0\) surface: \[ \frac{du_{0,j,k}(t)}{\partial t} = \alpha \nabla^2 u_{0,j,k}(t) + f_{0jk}(t) + \frac{h}{c\rho}(T_{\text{air}}-u_{0,j,k}) \] where

\[\begin{align*} \nabla^2 u_{0,j,k}(t) &= \frac{1}{\Delta x\Delta y\Delta z} \left(\Delta y \Delta z \frac{u_{1,j,k}(t) - u_{0,j,k}(t)}{\Delta x} \right. \\ &\qquad + \frac{\Delta x}{2} \Delta z \frac{u_{0,j-1,k}(t) + u_{0,j+1,k}(t) - 2 u_{0,j,k}(t)}{\Delta y} \\ &\qquad \left. + \frac{\Delta x}{2} \Delta y \frac{u_{0,j,k-1}(t) + u_{0,j,k+1}(t) - 2 u_{0,j,k}(t)}{\Delta z}\right) \end{align*}\]

This simplifies to:

\[\begin{align*} \nabla^2 u_{0,j,k}(t) = \frac{1}{2} &\left(\frac{2 u_{1,j,k}(t) - 2 u_{0,j,k}(t)}{\Delta x^2}\right. \\ &\qquad + \frac{u_{0,j-1,k}(t) + u_{0,j+1,k}(t) - 2 u_{0,j,k}(t)}{\Delta y^2} \\ &\qquad + \left. \frac{u_{0,j,k-1}(t) + u_{0,j,k+1}(t) - 2 u_{0,j,k}(t)}{\Delta z^2} \right) \\ \end{align*}\]

Again, with a uniform grid, this becomes: \[ \nabla^2 u_{0,j,k}(t) = \frac{2 u_{1,j,k}(t) + u_{0,j-1,k}(t) + u_{0,j+1,k}(t) + u_{0,j,k-1}(t) + u_{0,j,k+1}(t) - 6 u_{0,j,k}(t)}{2 \Delta x^2} \]

Following a similar method we can find for all 6 surfaces:

\[\begin{align*} \nabla^2 u_{0,j,k}(t) &= \frac{2 u_{1,j,k}(t) + u_{0,j-1,k}(t) + u_{0,j+1,k}(t) + u_{0,j,k-1}(t) + u_{0,j,k+1}(t) - 6 u_{0,j,k}(t)}{2 \Delta x^2} \\ \nabla^2 u_{I,j,k}(t) &= \frac{2 u_{I-1,j,k}(t) + u_{I,j-1,k}(t) + u_{I,j+1,k}(t) + u_{I,j,k-1}(t) + u_{I,j,k+1}(t) - 6 u_{I,j,k}(t)}{2 \Delta x^2} \\ \nabla^2 u_{i,0,k}(t) &= \frac{2 u_{i,1,k}(t) + u_{i-1,0,k}(t) + u_{i+1,0,k}(t) + u_{i,0,k-1}(t) + u_{i,0,k+1}(t) - 6 u_{i,0,k}(t)}{2 \Delta x^2} \\ \nabla^2 u_{i,J,k}(t) &= \frac{2 u_{i,J-1,k}(t) + u_{i-1,J,k}(t) + u_{i+1,J,k}(t) + u_{i,J,k-1}(t) + u_{i,J,k+1}(t) - 6 u_{i,J,k}(t)}{2 \Delta x^2} \\ \nabla^2 u_{i,j,0}(t) &= \frac{2 u_{i,j,1}(t) + u_{i-1,j,0}(t) + u_{i+1,j,0}(t) + u_{i,j-1,0}(t) + u_{i,j+1,0}(t) - 6 u_{i,j,0}(t)}{2 \Delta x^2} \\ \nabla^2 u_{i,j,K}(t) &= \frac{2 u_{i,j,K-1}(t) + u_{i,j-1,K}(t) + u_{i,j+1,K}(t) + u_{i,j,K}(t) + u_{i,j,k+1}(t) - 6 u_{i,j,K}(t)}{2 \Delta x^2} \\ \end{align*}\]

Heat equation on a boundary edge

So if we are considering the \(x=0, i=0\), \(y=0, j=0\) edge: \[ \frac{du_{0,0,k}(t)}{\partial t} = \alpha \nabla^2 u_{0,0,k}(t) + f_{0,0,k}(t) + \frac{h}{c\rho}(T_{\text{air}}-u_{0,0,k}) \] where

\[\begin{align*} \nabla^2 u_{0,0,k}(t) &= \frac{1}{\Delta x\Delta y\Delta z} \left(\frac{\Delta y}{2} \Delta z \frac{u_{1,0,k}(t) - u_{0,0,k}(t)}{\Delta x} \right. \\ &\qquad + \frac{\Delta x}{2} \Delta z \frac{u_{0,1,k}(t) - u_{0,0,k}(t)}{\Delta y} \\ &\qquad \left. + \frac{\Delta x}{2} \frac{\Delta y}{2} \frac{u_{0,0,k-1}(t) + u_{0,0,k+1}(t) - 2 u_{0,0,k}(t)}{\Delta z}\right) \\ \end{align*}\]

This simplifies to:

\[\begin{align*} \nabla^2 u_{0,0,k}(t) &= \frac{1}{4} \left(\frac{2u_{1,0,k}(t) - 2u_{0,0,k}(t)}{\Delta x^2} \right. \\ &\qquad + \frac{2u_{0,1,k}(t) - 2u_{0,0,k}(t)}{\Delta y^2} \\ &\qquad \left. + \frac{u_{0,0,k-1}(t) + u_{0,0,k+1}(t) - 2 u_{0,0,k}(t)}{\Delta z^2}\right) \\ \end{align*}\]

Again, with a uniform grid, this becomes: \[ \nabla^2 u_{0,0,k}(t) = \frac{2 u_{1,0,k}(t) + 2 u_{0,1,k}(t) + u_{0,0,k-1}(t) + u_{0,0,k+1}(t) - 6 u_{0,0,k}(t)}{4 \Delta x^2} \]

Following a similar method we can find for all 12 edges:

\[\begin{align*} \nabla^2 u_{0,0,k}(t) &= \frac{2 u_{1,0,k}(t) + 2 u_{0,1,k}(t) + u_{0,0,k-1}(t) + u_{0,0,k+1}(t) - 6 u_{0,0,k}(t)}{4 \Delta x^2} \\ \nabla^2 u_{0,J,k}(t) &= \frac{2 u_{1,J,k}(t) + 2 u_{0,J-1,k}(t) + u_{0,J,k-1}(t) + u_{0,J,k+1}(t) - 6 u_{0,J,k}(t)}{4 \Delta x^2} \\ \nabla^2 u_{0,j,0}(t) &= \frac{2 u_{1,j,0}(t) + 2 u_{0,j,1}(t) + u_{0,j-1,0}(t) + u_{0,j+1,0}(t) - 6 u_{0,j,0}(t)}{4 \Delta x^2} \\ \nabla^2 u_{0,j,K}(t) &= \frac{2 u_{1,j,K}(t) + 2 u_{0,j,K-1}(t) + u_{0,j-1,K}(t) + u_{0,j+1,0}(t) - 6 u_{0,j,K}(t)}{4 \Delta x^2} \\ \nabla^2 u_{I,0,k}(t) &= \frac{2 u_{I-1,0,k}(t) + 2 u_{I,1,k}(t) + u_{I,0,k-1}(t) + u_{I,0,k+1}(t) - 6 u_{I,0,k}(t)}{4 \Delta x^2} \\ \nabla^2 u_{I,J,k}(t) &= \frac{2 u_{I-1,J,k}(t) + 2 u_{I,J-1,k}(t) + u_{I,J,k-1}(t) + u_{I,J,k+1}(t) - 6 u_{I,J,k}(t)}{4 \Delta x^2} \\ \nabla^2 u_{I,j,0}(t) &= \frac{2 u_{I-1,j,0}(t) + 2 u_{I,j,1}(t) + u_{I,j-1,0}(t) + u_{I,j+1,0}(t) - 6 u_{I,j,0}(t)}{4 \Delta x^2} \\ \nabla^2 u_{I,j,K}(t) &= \frac{2 u_{I-1,j,K}(t) + 2 u_{I,j,K-1}(t) + u_{I,j-1,K}(t) + u_{I,j+1,K}(t) - 6 u_{I,j,K}(t)}{4 \Delta x^2} \\ \nabla^2 u_{i,0,0}(t) &= \frac{2 u_{i,0,1}(t) + 2 u_{i,1,0}(t) + u_{i-1,0,0}(t) + u_{i+1,0,0}(t) - 6 u_{i,0,0}(t)}{4 \Delta x^2} \\ \nabla^2 u_{i,0,K}(t) &= \frac{2 u_{i,0,K-1}(t) + 2 u_{i,1,K}(t) + u_{i-1,0,K}(t) + u_{i+1,0,K}(t) - 6 u_{i,0,K}(t)}{4 \Delta x^2} \\ \nabla^2 u_{i,J,0}(t) &= \frac{2 u_{i,J,1}(t) + 2 u_{i,J-1,0}(t) + u_{i-1,J,0}(t) + u_{i+1,J,0}(t) - 6 u_{i,J,0}(t)}{4 \Delta x^2} \\ \nabla^2 u_{i,J,K}(t) &= \frac{2 u_{i,J,K-1}(t) + 2 u_{i,J-1,K}(t) + u_{i-1,J,K}(t) + u_{i+1,J,K}(t) - 6 u_{i,J,K}(t)}{4 \Delta x^2} \\ \end{align*}\]

Heat equation on a boundary corner

So if we are considering the \(x=0, i=0\), \(y=0, j=0\), \(z=0, k=0\) corner: \[ \frac{du_{0,0,0}(t)}{\partial t} = \alpha \nabla^2 u_{0,0,0}(t) + f_{0,0,0}(t) + \frac{h}{c\rho}(T_{\text{air}}-u_{0,0,0}) \] where

\[\begin{align*} \nabla^2 u_{0,0,0}(t) &= \frac{1}{\Delta x\Delta y\Delta z} \left(\frac{\Delta y}{2} \frac{\Delta z}{2} \frac{u_{1,0,0}(t) - u_{0,0,0}(t)}{\Delta x} \right.\\ &\qquad + \frac{\Delta x}{2} \frac{\Delta z}{2} \frac{u_{0,1,0}(t) - u_{0,0,0}(t)}{\Delta y} \\ &\qquad \left. + \frac{\Delta x}{2} \frac{\Delta y}{2} \frac{u_{0,0,1}(t) - 2 u_{0,0,0}(t)}{\Delta z}\right) \\ \end{align*}\]

This simplifies to:

\[ \nabla^2 u_{0,0,0}(t) = \frac{1}{4} \left(\frac{u_{1,0,0}(t) - u_{0,0,0}(t)}{\Delta x^2} + \frac{u_{0,1,0}(t) - u_{0,0,0}(t)}{\Delta y^2} + \frac{u_{0,0,1}(t) - u_{0,0,0}(t)}{\Delta z^2}\right) \]

Again, with a uniform grid, this becomes: \[ \nabla^2 u_{0,0,0}(t) = \frac{u_{1,0,0}(t) + u_{0,1,0}(t) + u_{0,0,1}(t) - 3 u_{0,0,0}(t)}{2 \Delta x^2} \]

Following a similar method we can find for all 8 corners:

\[\begin{align*} \nabla^2 u_{0,0,0}(t) &= \frac{u_{1,0,0}(t) + u_{0,1,0}(t) + u_{0,0,1}(t) - 3 u_{0,0,0}(t)}{2 \Delta x^2} \\ \nabla^2 u_{I,0,0}(t) &= \frac{u_{I-1,0,0}(t) + u_{I,1,0}(t) + u_{I,0,1}(t) - 3 u_{I,0,0}(t)}{2 \Delta x^2} \\ \nabla^2 u_{0,J,0}(t) &= \frac{u_{1,J,0}(t) + u_{0,J-1,0}(t) + u_{0,J,1}(t) - 3 u_{0,J,0}(t)}{2 \Delta x^2} \\ \nabla^2 u_{0,0,K}(t) &= \frac{u_{1,0,K}(t) + u_{0,1,K}(t) + u_{0,0,K-1}(t) - 3 u_{0,0,K}(t)}{2 \Delta x^2} \\ \nabla^2 u_{I,J,0}(t) &= \frac{u_{I-1,J,0}(t) + u_{I,J-1,0}(t) + u_{I,J,1}(t) - 3 u_{I,J,0}(t)}{2 \Delta x^2} \\ \nabla^2 u_{I,0,K}(t) &= \frac{u_{I-1,0,K}(t) + u_{I,1,K}(t) + u_{I,0,K-1}(t) - 3 u_{I,0,K}(t)}{2 \Delta x^2} \\ \nabla^2 u_{0,J,K}(t) &= \frac{u_{1,J,K}(t) + u_{0,J-1,K}(t) + u_{0,J,K-1}(t) - 3 u_{0,J,K}(t)}{2 \Delta x^2} \\ \nabla^2 u_{I,J,K}(t) &= \frac{u_{I-1,J,K}(t) + u_{I,J-1,K}(t) + u_{I,J,K-1}(t) - 3 u_{I,J,K}(t)}{2 \Delta x^2} \\ \end{align*}\]

These are all coded into the function below.

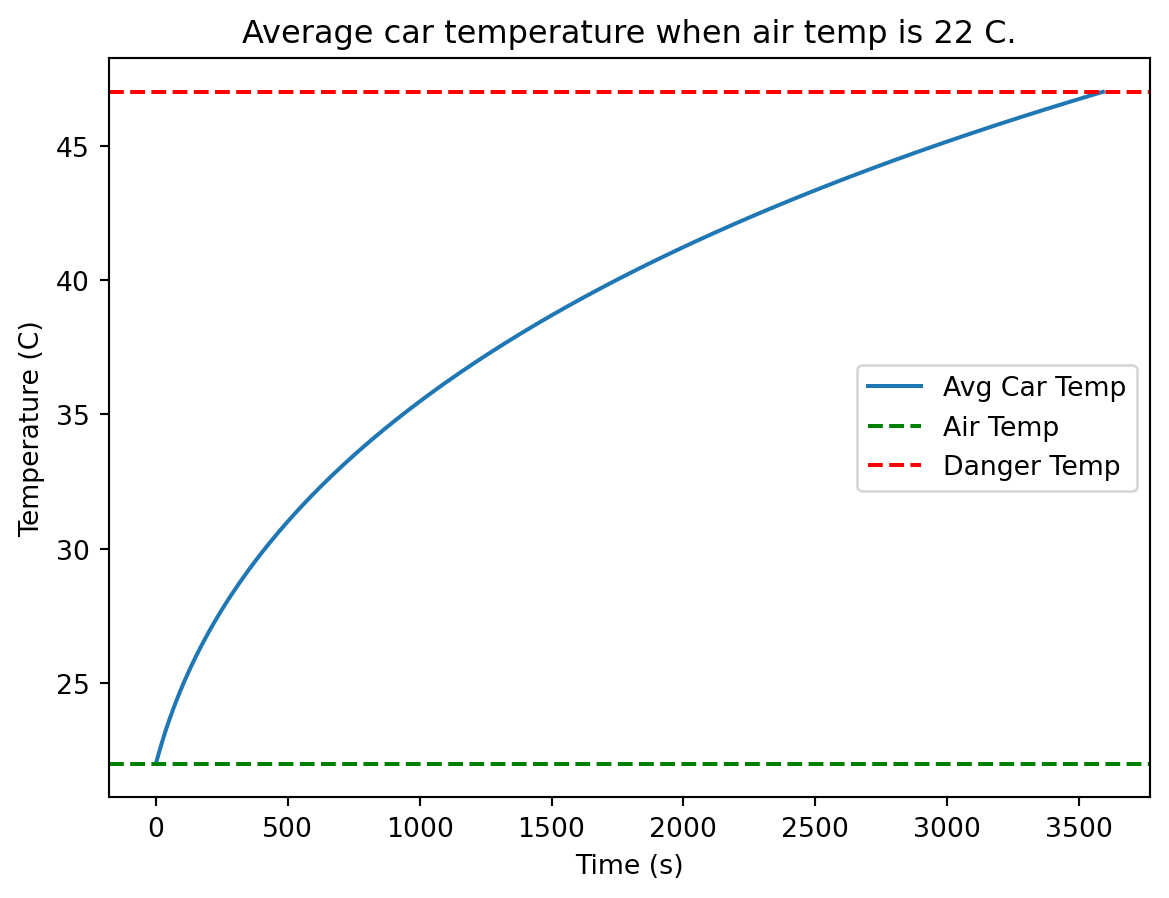
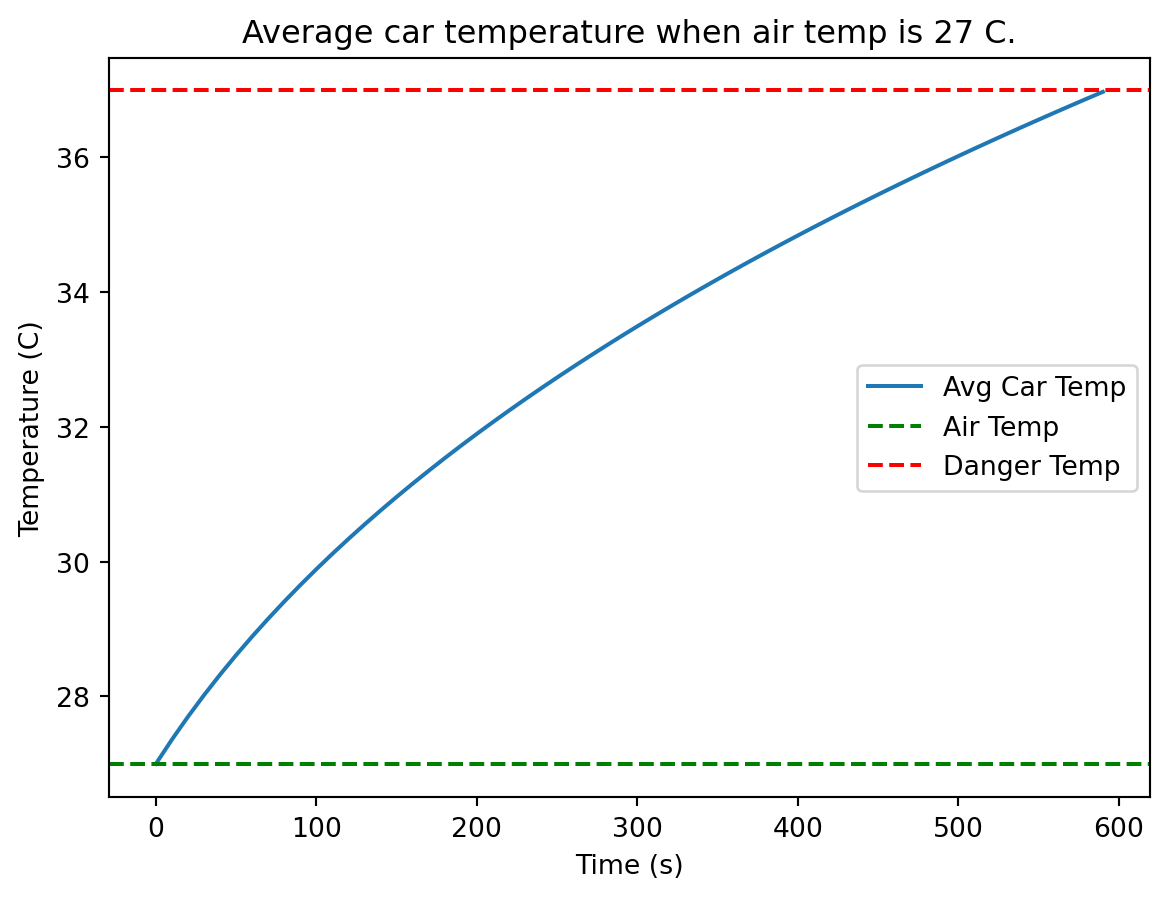
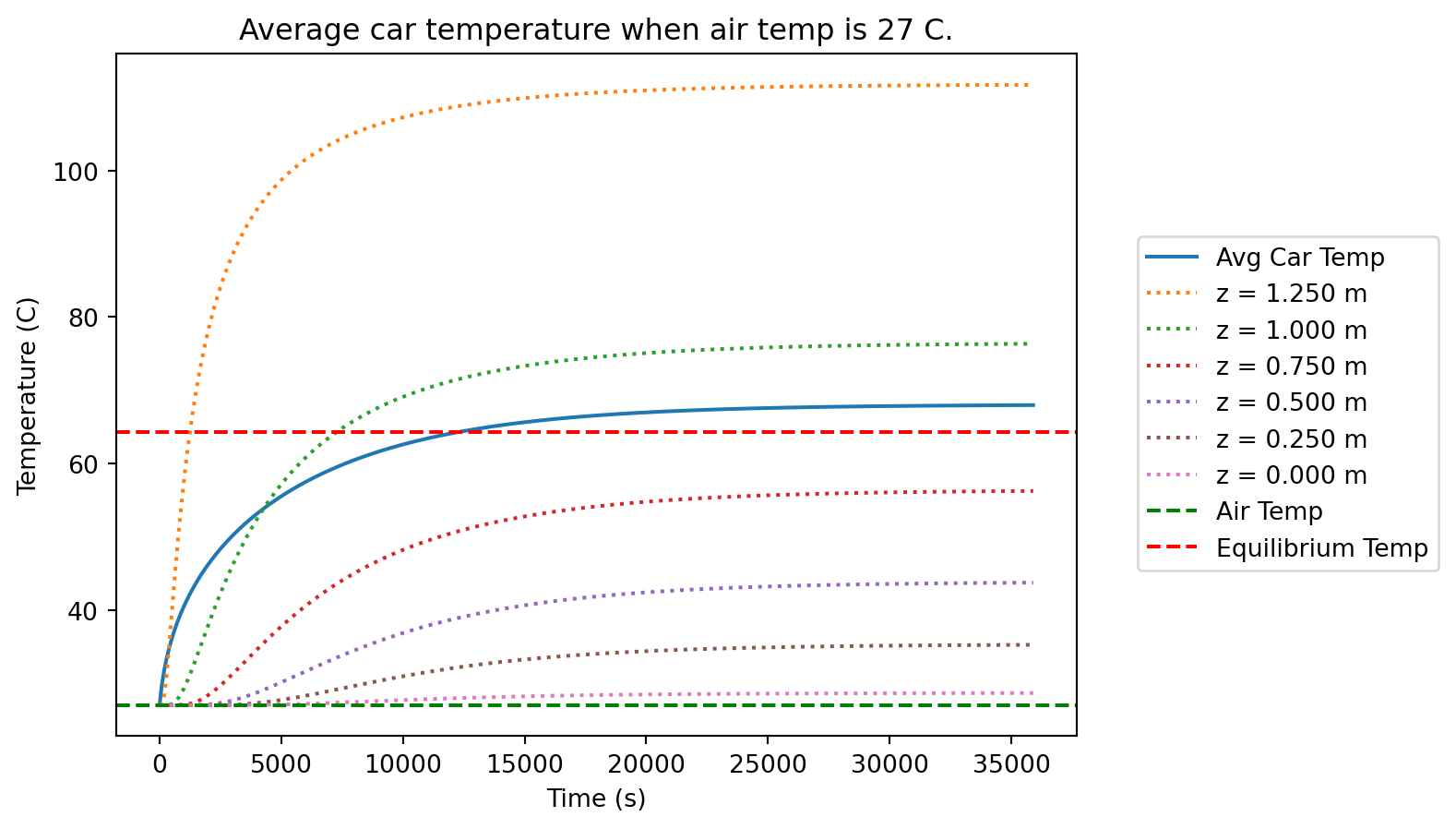
def lap3DFE(umat,dx):
    lap = np.empty_like(umat)

    # Interior elements:
    lap[1:-1,1:-1,1:-1] = (umat[:-2, 1:-1, 1:-1] + umat[2:, 1:-1, 1:-1] + umat[1:-1, :-2, 1:-1] + 
                           umat[1:-1, 2:, 1:-1] + umat[1:-1,1:-1,:-2] + umat[1:-1,1:-1,2:] - 6*umat[1:-1,1:-1,1:-1]) / dx**2

    # Surface elements:
    lap[0,1:-1,1:-1] = (2*umat[1, 1:-1, 1:-1] + umat[0, :-2, 1:-1] + umat[0, 2:, 1:-1] + umat[0, 1:-1, :-2] + umat[0, 1:-1, 2:] - 
        6*umat[0, 1:-1, 1:-1]) / (2*dx**2)
    lap[-1,1:-1,1:-1] = (2* umat[-2, 1:-1, 1:-1] + umat[-1, :-2, 1:-1] + umat[-1, 2:, 1:-1] + umat[-1, 1:-1, :-2] + umat[-1, 1:-1, 2:] -
        6*umat[-1, 1:-1, 1:-1]) / (2*dx**2)
    lap[1:-1,0,1:-1] = (2* umat[1:-1, 1, 1:-1] + umat[:-2, 0, 1:-1] + umat[2:, 0, 1:-1] + umat[1:-1, 0, :-2] + umat[1:-1, 0, 2:] - 
        6*umat[1:-1, 0, 1:-1]) / (2*dx**2)
    lap[1:-1,-1,1:-1] = (2* umat[1:-1, -2, 1:-1] + umat[:-2, -1, 1:-1] + umat[2:, -1, 1:-1] + umat[1:-1, -1, :-2] + umat[1:-1, -1, 2:] - 
        6*umat[1:-1, -1, 1:-1]) / (2*dx**2)
    lap[1:-1,1:-1,0] = (2* umat[1:-1, 1:-1, 1] + umat[:-2, 1:-1, 0] + umat[2:, 1:-1, 0] + umat[1:-1, :-2, 0] + umat[1:-1, 2:, 0] - 
        6*umat[1:-1, 1:-1, 0]) / (2*dx**2)
    lap[1:-1,1:-1,-1] = (2* umat[1:-1, 1:-1, -2] + umat[:-2, 1:-1, -1] + umat[2:, 1:-1, -1] + umat[1:-1, :-2, -1] + umat[1:-1, 2:, -1] - 
        6*umat[1:-1, 1:-1, -1]) / (2*dx**2)

    # Edge Elements:
    lap[0,0,1:-1] = (2 * umat[1, 0, 1:-1] + 2 * umat[0, 1, 1:-1] + umat[0, 0, :-2] + umat[0, 0, 2:] - 6*umat[0, 0, 1:-1]) / (4*dx**2)
    lap[0,-1,1:-1] = (2 * umat[1, -1, 1:-1] + 2 * umat[0, -2, 1:-1] + umat[0, -1, :-2] + umat[0, -1, 2:] - 6*umat[0, -1, 1:-1]) / (4*dx**2)
    lap[-1,0,1:-1] = (2 * umat[-2, 0, 1:-1] + 2 * umat[-1, 1, 1:-1] + umat[-1, 0, :-2] + umat[-1, 0, 2:] - 6*umat[-1, 0, 1:-1]) / (4*dx**2)
    lap[-1,-1,1:-1] = (2 * umat[-2, -1, 1:-1] + 2 * umat[-1, -2, 1:-1] + umat[-1, -1, :-2] + umat[-1, -1, 2:] - 6*umat[-1, -1, 1:-1]) / (4*dx**2)
    lap[0,1:-1,0] = (2 * umat[1, 1:-1, 0] + 2 * umat[0, 1:-1, 1] + umat[0, 2:, 0] + umat[0, :-2, 0] - 6*umat[0, 1:-1, 0]) / (4*dx**2)
    lap[0,1:-1,-1] = (2 * umat[1, 1:-1, -1] + 2 * umat[0, 1:-1, -2] + umat[0, 2:, -1] + umat[0, :-2, -1] - 6*umat[0, 1:-1, -1]) / (4*dx**2)
    lap[-1,1:-1,0] = (2 * umat[-2, 1:-1, 0] + 2 * umat[-1, 1:-1, 1] + umat[-1, 2:, 0] + umat[-1, :-2, 0] - 6*umat[-1, 1:-1, 0]) / (4*dx**2)
    lap[-1,1:-1,-1] = (2 * umat[-2, 1:-1, -1] + 2 * umat[-1, 1:-1, -2] + umat[-1, 2:, -1] + umat[-1, :-2, -1] - 6*umat[-1, 1:-1, -1]) / (4*dx**2)
    lap[1:-1,0,0] = (2 * umat[1:-1, 1, 0] + 2 * umat[1:-1, 0, 1] + umat[:-2, 0, 0] + umat[2:, 0, 0] - 6*umat[1:-1, 0, 0]) / (4*dx**2)
    lap[1:-1,0,-1] = (2 * umat[1:-1, 1, -1] + 2 * umat[1:-1, 0, -2] + umat[:-2, 0, -1] + umat[2:, 0, -1] - 6*umat[1:-1, 0, -1]) / (4*dx**2)
    lap[1:-1,-1,0] = (2 * umat[1:-1, -2, 0] + 2 * umat[1:-1, -1, 1] + umat[:-2, -1, 0] + umat[2:, -1, 0] - 6*umat[1:-1, -1, 0]) / (4*dx**2)
    lap[1:-1,-1,-1] = (2 * umat[1:-1, 2, -1] + 2 * umat[1:-1, -1, -2] + umat[:-2, -1, -1] + umat[2:, -1, -1] - 6*umat[1:-1, -1, -1]) / (4*dx**2)    
    
    # Corner Elements:
    lap[0,0,0] = (umat[1, 0, 0] + umat[0, 1, 0] + umat[0, 0, 1] - 3*umat[0, 0, 0]) / (2*dx**2)
    lap[-1,0,0] = (umat[-2, 0, 0] + umat[-1, 1, 0] + umat[-1, 0, 1] - 3*umat[-1, 0, 0]) / (2*dx**2)
    lap[0,-1,0] = (umat[1, -1, 0] + umat[0, -2, 0] + umat[0, -1, 1] - 3*umat[0, -1, 0]) / (2*dx**2)
    lap[0,0,-1] = (umat[1, 0, -1] + umat[0, 1, -1] + umat[0, 0, -2] - 3*umat[0, 0, -1]) / (2*dx**2)
    lap[0,-1,-1] = (umat[1, -1, -1] + umat[0, -2, -1] + umat[0, -1, -2] - 3*umat[0, -1, -1]) / (2*dx**2)
    lap[-1,0,-1] = (umat[-2, 0, -1] + umat[-1, 1, -1] + umat[-1, 0, -2] - 3*umat[-1, 0, -1]) / (2*dx**2)
    lap[-1,-1,0] = (umat[2, -1, 0] + umat[-1, -2, 0] + umat[-1, -1, 1] - 3*umat[-1, -1, 0]) / (2*dx**2)
    lap[-1,-1,-1] = (umat[-2, -1, -1] + umat[-1, -2, -1] + umat[-1, -1, -2] - 3*umat[-1, -1, -1]) / (2*dx**2)

    return lap

Final Heat equation function

def dudt(t,u, alpha, intensity, dx, Tair, A, B):
    dudt = alpha*lap3DFE(u,dx) + powerGen(u, t, intensity, A) + bdryConv(u, t, Tair, B)
    return dudt

I will have to flatten things as solve_ivp only solves a vector system of differential equations rather than the higher dimenionality matrix system that I’ve created.

def dudtFlat(t,uflat, alpha, intensity, dx, Tair, A, B):
    u = uflat.reshape(xmax,ymax,zmax)
    return dudt(t,u, alpha, intensity, dx, Tair, A, B).flatten()

Analysis plan

I will begin by choosing parameters \(A\) and \(B\) based on an initial guess, and then I will adjust those parameters to minimize the absolute difference between the result that I obtain and the target temperatures noted in these statements

• When it’s 22 degrees Celsius outside, the temperature inside your car can heat up to 47 degrees Celsius within an hour.
• When it’s 27 degrees Celsius outside, the temperature inside your car can heat up to 37 degrees Celsius within 10 minutes.

Calculation 1:

For parameters \(A\) and \(B\) (described above) find the difference between the average box temperature after an hour and 47 deg C, assuming an air temperature of 22 deg C.

import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

def calc1(A,B):
    oneHour = 3600
    airTemp = 22
    hotCarTemp = 47
    u0.fill(airTemp)
    time = np.arange(0,oneHour,10)
    
    oneHourCalc = solve_ivp(dudtFlat, t_span=[0,oneHour], y0=u0.flatten(), t_eval= time, 
                            args=[thermalDiffusivity,solarIntensity,Deltax,airTemp,A,B])
    
    avgBoxTempCalc = np.mean(oneHourCalc.y,axis=0)

    finalAvgTemp = avgBoxTempCalc[-1]
    tempDiff = finalAvgTemp - hotCarTemp

    return tempDiff

Calculation 2:

For parameters \(A\) and \(B\) (described above) find the difference between the average box temperature after 10 minutes and 37 deg C, assuming an air temperature of 27 deg C.

def calc2(A,B):
    tenMin = 60*10
    airTemp = 27
    hotCarTemp = 37
    u0.fill(airTemp)
    time = np.arange(0,tenMin,10)
    
    tenMinCalc = solve_ivp(dudtFlat, t_span=[0,tenMin], y0=u0.flatten(), t_eval= time, 
                            args=[thermalDiffusivity,solarIntensity,Deltax,airTemp,A,B])
    
    avgBoxTempCalc = np.mean(tenMinCalc.y,axis=0)

    finalAvgTemp = avgBoxTempCalc[-1]
    tempDiff = finalAvgTemp - hotCarTemp

    return tempDiff

Optimization

Now I will find the parameters \(A\) and \(B\) that correctly model the statements given in the opening section of this post.

from scipy.optimize import minimize
from scipy.optimize import Bounds

bounds = ((0, None), (0, None))

def totalTempDiff(x):
    A, B = x
    diff1 = np.abs(calc1(A,B))
    diff2 = np.abs(calc2(A,B))
    diff = diff1+diff2
    return diff

estA = 1/(specificHeat*wallDensity*(Deltax/10))
estB = heatTransferCoef/(specificHeat*wallDensity*(Deltax/1000))
x0 = np.array([estA,estB])

res = minimize(totalTempDiff,x0,bounds=bounds)

A,B = res.x
diff1 = np.abs(calc1(A,B))
diff2 = np.abs(calc2(A,B))

print(f'The temperature differences are {diff1:.3f} deg C for calculation 1 and {diff2:.3f} deg C for calculation 2')

The temperature differences are 0.000 deg C for calculation 1 and 0.030 deg C for calculation 2

Since we can interpret the parameters \(A\) and \(B\) through the properties of materials, as described above, we find:

print(f'A = {res.x[0]:2e} m^2K/Ws and B= {res.x[1]:2e} 1/s')

D = 1/(specificHeat*wallDensity*res.x[0])
Delta = heatTransferCoef/(specificHeat*wallDensity*res.x[1])
print(f'δ = {D:.5f} m and Δ = {Delta:.5f} m.')

A = 1.117617e-03 m^2K/Ws and B= 6.666691e-03 1/s
δ = 0.00030 m and Δ = 0.00005 m.

Plot the time evolution of the temperature

Finally, I’ll plot the time evolution of the average temperature for these systems.

def plot1(A,B):
    oneHour = 3600
    airTemp = 22
    hotCarTemp = 47
    u0.fill(airTemp)
    time = np.arange(0,oneHour,10)
    
    oneHourCalc = solve_ivp(dudtFlat, t_span=[0,oneHour], y0=u0.flatten(), t_eval= time, 
                            args=[thermalDiffusivity,solarIntensity,Deltax,airTemp,A,B])
    
    avgBoxTempCalc = np.mean(oneHourCalc.y,axis=0)

    plt.plot(time,avgBoxTempCalc,label='Avg Car Temp')
    plt.axhline(y=airTemp,label='Air Temp',ls='--',color='green')
    plt.axhline(y=hotCarTemp,label='Danger Temp',ls='--',color='red')
    plt.title(f'Average car temperature when air temp is {airTemp:.0f} C.') 
    plt.xlabel('Time (s)')
    plt.ylabel('Temperature (C)')
    plt.legend()
    plt.show()

def plot2(A,B):
    tenMin = 60*10
    airTemp = 27
    hotCarTemp = 37
    u0.fill(airTemp)
    time = np.arange(0,tenMin,10)
    
    tenMinCalc = solve_ivp(dudtFlat, t_span=[0,tenMin], y0=u0.flatten(), t_eval= time, 
                            args=[thermalDiffusivity,solarIntensity,Deltax,airTemp,A,B])
    
    avgBoxTempCalc = np.mean(tenMinCalc.y,axis=0)

    plt.plot(time,avgBoxTempCalc,label='Avg Car Temp')
    plt.axhline(y=airTemp,label='Air Temp',ls='--',color='green')
    plt.axhline(y=hotCarTemp,label='Danger Temp',ls='--',color='red')
    plt.title(f'Average car temperature when air temp is {airTemp:.0f} C.') 
    plt.xlabel('Time (s)')
    plt.ylabel('Temperature (C)')
    plt.legend()
    plt.show()

A,B = res.x
plot1(A,B)
plot2(A,B)

This makes sense. In both systems the rate of heating decreases with time, suggesting that there is an upper limit to the temperature that the box will approach. Note that we need to put the ratio of the area of the top surface to the total surface area of the box in front of the solar generation term as the box is only gaining area through the top surface in this model, while convection is occurring everywhere on the surface of the box.

\[ \frac{du}{dt} = \alpha\nabla^2u + AI_s + B(T_{\text{air}}-u) \longrightarrow 0 = 0 + \frac{A_{\text{top}}}{A_{\text{box}}} AI_s + B(T_{\text{air}}-u_0) \] Solving for the equilibrium temperature, we find: \[ \implies u_0 = T_{\text{air}} + \left(\frac{A_{\text{top}}}{A_{\text{box}}}\right) \frac{AI_s}{B} \]

Given the system that I’m modeling, and values for \(A\) and \(B\) that I have found, we can calculate the difference between air temperature and the steady-state box temperature.

topArea = L*W
boxArea = 2*(L*W + L*H + W*H)
solarBoost = A * solarIntensity/B * topArea/boxArea
print(f'The temperature after a long time should approach a value that is {solarBoost:.2f} deg C warmer than the air temperature.')

The temperature after a long time should approach a value that is 37.25 deg C warmer than the air temperature.

Let’s verify this calculation by simulating this system for 10 hours.

def simSystem(A,B):
    oneHour = 3600
    airTemp = 27
    eqTemp = airTemp + A*solarIntensity/B * L*W/(2*(L*W + L*H + W*H))
    u0.fill(airTemp)
    time = np.arange(0,10*oneHour,100)
    
    oneHourCalc = solve_ivp(dudtFlat, t_span=[0,10*oneHour], y0=u0.flatten(), t_eval= time, 
                            args=[thermalDiffusivity,solarIntensity,Deltax,airTemp,A,B])
    return oneHourCalc

longCalc = simSystem(A,B)    

And then I will plot the average temperature as a function of time, as well as the average temperature at a range of heights.

def plotTemperature(uflat):
    oneHour = 3600
    airTemp = 27
    eqTemp = airTemp + A*solarIntensity/B * L*W/(2*(L*W + L*H + W*H))
    time = np.arange(0,10*oneHour,100)
    avgBoxTempCalc = np.mean(uflat,axis=0)
    avgBoxTempZ = np.empty((len(time),zmax))
    
    for l in range(len(time)):
      umat = uflat[:, l].reshape((xmax,ymax,zmax))
      for k in range(zmax):
        avgBoxTempZ[l,k] = np.mean(umat[:,:,k])
      

    plt.plot(time,avgBoxTempCalc,label='Avg Car Temp')
    for k in reversed(range(0, zmax, 5)):
      zdim = k * Deltax
      labText = f'z = {zdim:.3f} m'
      plt.plot(time, avgBoxTempZ[:,k],label=labText,ls='dotted')
    plt.axhline(y=airTemp,label='Air Temp',ls='--',color='green')
    plt.axhline(y=eqTemp,label='Equilibrium Temp',ls='--',color='red')
    plt.title(f'Average car temperature when air temp is {airTemp:.0f} C.') 
    plt.xlabel('Time (s)')
    plt.ylabel('Temperature (C)')
    plt.legend(bbox_to_anchor=(1.05,0.75))
    plt.show()
    
plotTemperature(longCalc.y)

As we see that the temperature is not uniform at every point in the hot box, it becomes clear that assumption of uniform temperature is not appropriate. Since we see there is still a temperature gradient along the z-direction, conduction is still important in this system, and contributes to the equilibrium. Still this rough approximation gave a good intuition about the dynamics of the system even if it wasn’t numerically accurate.

Note, this assumes that the sun stays at “high noon” for at least 10 hours, so it isn’t representative of a real car on the surface of the earth. As such, it’s not worth exploring this further, except for the purposes of developing better visualizations.

Coming soon

So far, this has been lots of equations, and not enough pictures. But this is a complex system, and I need to add one feature at a time to ensure that it is working correctly. My first order of business will be to make a surface heat map of what is going on so that it is easier to talk about and show everyone what is going on.

I also need to develop code which allows for the sun to change it’s position. And I’ll deal with other issues such as seasonal changes/the varying length of day/night. As well as deal with latitude. I’ve been fiddling with the math on the back of napkins, and that should work nicely with some pretty pictures. Then we can compare hot boxes in higher latitudes to those with lower latitudes.